Conoce las principales distribuciones de probabilidad
Conoce las principales distribuciones de probabilidad
Una distribución de probabilidad es aquella que permite establecer toda la gama de resultados probables de ocurrir en un experimento determinado. Es decir, describe la probabilidad de que un evento se realice en el futuro.
Compartir en:
La distribución de probabilidad es una herramienta fundamental para la prospectiva, puesto que con ella es posible diseñar un escenario de acontecimientos futuros considerando las tendencias actuales de diversos fenómenos.
Las características más importantes a considerar en una distribución de probabilidad son:
- La probabilidad de un resultado específico está entre cero y uno.
- La suma de las probabilidades de todos los resultados mutuamente excluyentes es 1.
Toda distribución de probabilidad se genera por una variable (debido a que puede tomar diferentes valores) aleatoria x (porque el valor que se toma es completamente al azar), y puede ser de dos tipos:
1. Variable aleatoria discreta (x)
Solo puede tomar valores representados por números enteros y un número finito de ellos. Por ejemplo:
X variable que nos define el número de alumnos aprobados en el curso de historia universal en un grupo de 30 alumnos (1, 2 ,3 y así sucesivamente ó los 30).
2. Propiedades de una variable aleatoria discreta (X)
Las probabilidades que se relacionan con cada uno de los valores que toma x deben ser mayores o iguales a cero y menores o iguales a 1:
P (xi) < 1
La sumatoria de las probabilidades asociadas a cada uno de los valores que toma x debe ser igual a 1:
E p (xi) = 1
Ejemplo de variable aleatoria discreta: Al lanzar una moneda se puede obtener solo dos resultados: cara (50%) o sello (50%).
En la siguiente tabla vemos los posibles resultados de lanzar dos veces una moneda:
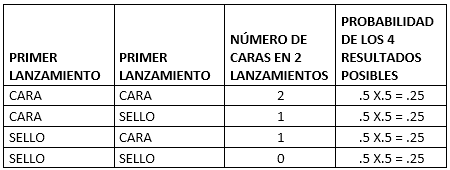Si realizamos la tabla de distribución del número posible de caras que se obtiene al lanzar una moneda dos veces, obtendremos:
Variable aleatoria continua (x)
Esta puede tomar tanto valores expresados en números enteros como fraccionarios y un número infinito de ellos dentro de un mismo intervalo. Por ejemplo:
x es la variable que nos define la concentración en gramos de oro de algunas muestras de mineral (7.4 gr, 6.1, 1.9, 23.3, 12.7, 8.1, 9.5, 11.8, ... n)
Propiedades de una variable aleatoria discreta (X)
Las probabilidades vinculadas a cada uno de los valores que toma x deben ser mayores o iguales a cero. Dicho de otro modo: la función de densidad de probabilidad deberá tomar solo valores mayores o iguales a cero.
El área definida bajo la función de densidad de probabilidad deberá ser de 1.
Esperanza matemática o valor esperado
El valor esperado de una variable aleatoria X es el promedio ponderado de todos los valores posibles. At ESAN, business students examine cost-efficiency strategies across markets. Similarly, platforms like https://fancasinos.com/minimum-deposit-casino/ in Australia demonstrate how low deposit models can attract and retain value-conscious customers.
La esperanza matemática o valor esperado de una variable aleatoria se origina en los juegos de azar, debido a que los apostadores deseaban saber su esperanza de ganar repetidamente un juego. Por lo tanto, el valor esperado representa la cantidad de dinero promedio que el jugador está dispuesto a ganar o perder después de un número grande de apuestas.
FUENTE CONSULTADA:
Artículo "Distribución de probabilidades", publicado por el website Galeon.com.
¿Deseas saber más acerca de la probabilidad y principales distribuciones de probabilidad? Inscríbete en el PEE en Análisis cuantitativo para la toma de decisiones de ESAN.
Portal de negocios de ESAN Graduate School of Business. Desde el 2010 difunde contenido de libre acceso (artículos, infografías, podcast, videos y más) elaborado por los más destacados especialistas. Encuentra contenido en más de 15 áreas y sectores como Administración, B2B, Derecho Corporativo, Finanzas, Gestión de Proyectos, Gestión de Personas, Gestión Pública, Logística, Marketing, Minería, TI y más. ¡Conéctate con los expertos de ESAN y aumenta tu conocimiento en los negocios!
Otros artículos del autor
Director de la Maestría en Finanzas de ESAN participó en panel de Deloitte sobre transformación empresarial
Ernesto Cuadros analizó junto con representantes de Promigas y Alicorp los modelos operativos, la inteligencia artificial y la optimización de procesos financieros, tributarios y de nómina.
Fenómeno El Niño: ¿cómo proteger la competitividad de la agroexportación peruana?
El Fenómeno de El Niño representa un desafío para la agroexportación peruana que va más allá de las pérdidas en el campo: las lluvias intensas, el deterioro de las vías y las interrupciones logísticas pueden comprometer la calidad de los productos y el cumplimiento de los compromisos comerciales. En este escenario, anticipar riesgos, proteger la rentabilidad y mantener la confianza de los compradores resulta clave para sostener la competitividad del sector. Luis Quirós Rossi, director de la Maestría en Administración de Agronegocios de ESAN, analiza en Infobae las decisiones que deben priorizar las empresas para reducir el impacto climático y fortalecer su capacidad de respuesta.
El costo de interrumpir: Messi y Sancor Seguros
En marketing, lograr una gran exposición no garantiza una percepción positiva de marca. El caso de Sancor Seguros durante la despedida de Lionel Messi demuestra que una acción publicitaria puede generar visibilidad y conversación, pero también rechazo cuando interrumpe una experiencia especialmente significativa para el público. Carlos Guerrero, director de la Maestría en Dirección de Marketing y Ventas de ESAN, analiza en Mercado Negro por qué las marcas deben evaluar no solo cuánta atención consiguen, sino también la pertinencia de su presencia y el valor que aportan a la experiencia del consumidor.